Leetcode 851 Loud and Rich

发表于 |

In a group of N people (labelled 0, 1, 2, …, N-1), each person has different amounts of money, and different levels of quietness.
For convenience, we’ll call the person with label x, simply “person x”.
We’ll say that richer[i] = [x, y] if person x definitely has more money than person y. Note that richer may only be a subset of valid observations.
Also, we’ll say quiet[x] = q if person x has quietness q.
Now, return answer, where answer[x] = y if y is the least quiet person (that is, the person y with the smallest value of quiet[y]), among all people who definitely have equal to or more money than person x.

Example 1:
Input: richer = [[1,0],[2,1],[3,1],[3,7],[4,3],[5,3],[6,3]], quiet = [3,2,5,4,6,1,7,0]
Output: [5,5,2,5,4,5,6,7]
Explanation:
answer[0] = 5.
Person 5 has more money than 3, which has more money than 1, which has more money than 0.
The only person who is quieter (has lower quiet[x]) is person 7, but
it isn’t clear if they have more money than person 0.
answer[7] = 7.
Among all people that definitely have equal to or more money than person 7
(which could be persons 3, 4, 5, 6, or 7), the person who is the quietest (has lower quiet[x])
is person 7.
The other answers can be filled out with similar reasoning.

Note:
1 <= quiet.length = N <= 500
0 <= quiet[i] < N, all quiet[i] are different.
0 <= richer.length <= N * (N-1) / 2
0 <= richer[i][j] < N
richer[i][0] != richer[i][1]
richer[i]’s are all different.
The observations in richer are all logically consistent.

分析：

  1. 人的编号从0到n-1，每个人有一定的钱和度，并且都不相同
  2. 返回ans，ans[i]代表比i这个人钱多的人中，度最小的人的编号
  3. 数据（节点）长度500，边长度不超过250000，故显然对边分析时，n^2复杂度不可行

思路：
对于每个人可以直接用dfs找，但是也得用dp存一下。topsort也是一样，都得用dp。由于我对dfs还是运用不到位，这里先写下topsort方法吧。
对于example中的例子，关系如图：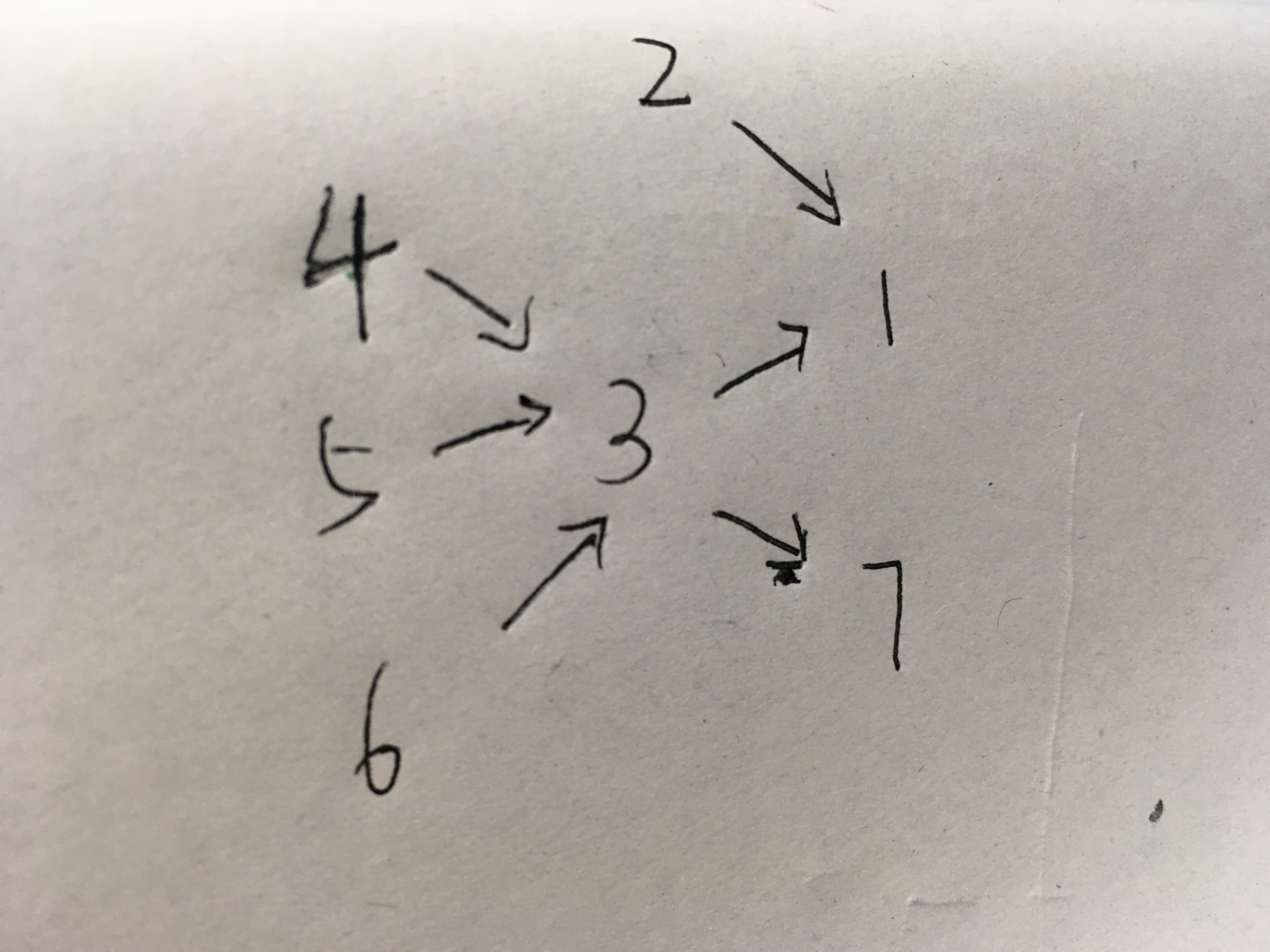

可以看到2，4，5，6入度为0，即没有比他们更多钱的人，那么对于这种节点 ,ans[i] = i
对于3,则要从指向他的节点（4，5，6）以及他自身中找到quiet值最小的点index,ans[3] = min(3,4,5,6,key=lambda x: quiet[ans[x]]) ,依次类推即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import collections,Queue
def loudAndRich(richer, quiet):
	# 存储形式 节点： 指向该节点的节点
	d = collections.defaultdict(list)
	# 存储形式 节点： 该节点指向的节点
	d1 = collections.defaultdict(list)
	# 记录入度
	count = [0] * len(quiet)
	ans = [float('inf')] * len(quiet)

	for x,y in richer:
		count[y] += 1
		d[y].append(x)
		d1[x].append(y)
	# 取入度为0的点
	Q = Queue.deque([i for i in range(len(quiet)) if count[i] == 0])
	while Q:
		node = Q.popleft()
		# 先默认结果为自身，然后和指向自身的节点依次比较
		res = node
		for e in d[node]:
			if quiet[ans[e]] < quiet[res]:
				res = ans[e]
		ans[node] = res
		# 修改入度，将入度变为0的节点加入队列
		for i in d1[node]:
			count[i] -= 1
			if count[i] == 0:
				Q.append(i)
	return ans


86 / 86 test cases passed.
difficulty: medium
Runtime: 256 ms