Leetcode 529 Minesweeper

发表于 |

让我们一起来玩扫雷游戏！
给定一个代表游戏板的二维字符矩阵。 ‘M’ 代表一个未挖出的地雷，’E’ 代表一个未挖出的空方块，’B’ 代表没有相邻（上，下，左，右，和所有4个对角线）地雷的已挖出的空白方块，数字（’1’ 到 ‘8’）表示有多少地雷与这块已挖出的方块相邻，’X’ 则表示一个已挖出的地雷。
现在给出在所有未挖出的方块中（’M’或者’E’）的下一个点击位置（行和列索引），根据以下规则，返回相应位置被点击后对应的面板：

  1. 如果一个地雷（’M’）被挖出，游戏就结束了- 把它改为 ‘X’。
  2. 如果一个没有相邻地雷的空方块（’E’）被挖出，修改它为（’B’），并且所有和其相邻的方块都应该被递归地揭露。
  3. 如果一个至少与一个地雷相邻的空方块（’E’）被挖出，修改它为数字（’1’到’8’），表示相邻地雷的数量。
  4. 如果在此次点击中，若无更多方块可被揭露，则返回面板。


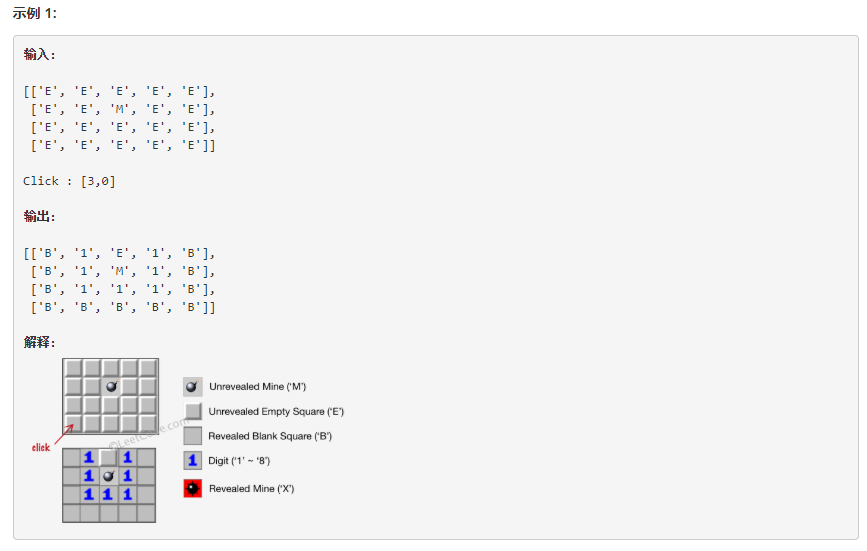
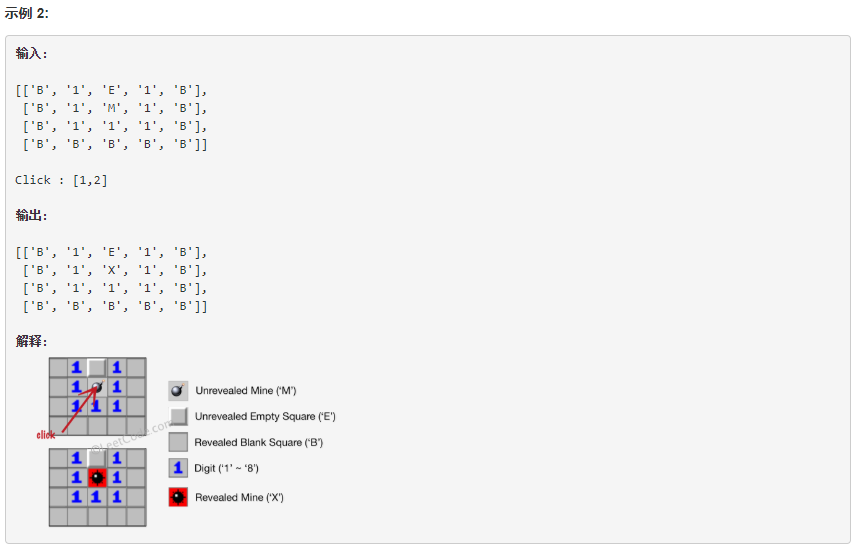
注意:

  1. 输入矩阵的宽和高的范围为 [1,50]。
  2. 点击的位置只能是未被挖出的方块 (‘M’ 或者 ‘E’)，这也意味着面板至少包含一个可点击的方块。
  3. 输入面板不会是游戏结束的状态（即有地雷已被挖出）。
  4. 简单起见，未提及的规则在这个问题中可被忽略。例如，当游戏结束时你不需要挖出所有地雷，考虑所有你可能赢得游戏或标记方块的情况。

分析：

  1. 根据规则中所述，关键有以下几点
    1. 点击处必为’E’或’M’，若是’M’，将其改为’X’游戏结束
    2. 若点击处为’E’，则判断’E’周围是否有雷存在，若有则返回雷的数量，将其修改为雷的数量
    3. 若’E’周围无雷，则对’E’周围格子（共8个）依次按照上述规则递归
  2. 这里举个简单例子，若点击(0,0)：(不能越过数字去递归(0,2)，这一点从示例1中也能看出)
    [E,E,E]————>[B,1,E]
    [E,E,M]————>[B,1,M]

思路：

  1. 当我们递归E的时候如何判断周边是否有雷呢，每次都遍历8个方向会有大量重复工作，虽然在这道题中即使你这样做也可以通过，但是显然这不是我们追求的
  2. 我们使用一个字典d[(i,j)]来存储(i,j)处周围的雷数量，那么容易想到我先遍历每一个雷，然后对雷周围的格子在d中进行一次变换存储
  3. 这样我们之后递归E时便可通过判断(i,j)是否存在于d中来判断E周边是否有雷
  4. 本身递归的dfs是很简单的，这里不做详细说明了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution(object):
    def updateBoard(self, board, click):
        """
        :type board: List[List[str]]
        :type click: List[int]
        :rtype: List[List[str]]
        """
        m,n = len(board),len(board[0])
        d = collections.defaultdict(int)
        directions = [(i-1,j-1),(i-1,j),(i-1,j+1),(i,j-1),(i,j+1),(i+1,j-1),(i+1,j),(i+1,j+1)]
        click_i,click_j = click
        # 点击处为雷
        if board[click_i][click_j] == 'M':
            board[click_i][click_j] = 'X'
            return board
        # 初始化字典
        def setNum(i,j,d):
            for x,y in directions:
                if 0<=x<m and 0<=y<n and board[x][y] != 'M':
                    d[(x,y)] += 1
        for i in range(m):
            for j in range(n):
                if board[i][j] == 'M':
                    setNum(i,j,d)
        # 点击处周边有雷
        if (click_i,click_j) in d:
            board[click_i][click_j] = str(d[(click_i,click_j)])
            return board
        # dfs依次递归
        visited = set()
        def dfs(i,j):
            visited.add((i,j))
            # 递归到数字则修改board
            if (i,j) in d: 
                board[i][j] = str(d[(i,j)])
                return
            else:
                board[i][j] = 'B'
            for x,y in directions:
                if 0<=x<m and 0<=y<n and (x,y) not in visited:
                    dfs(x,y)

        dfs(click_i,click_j)
        return board

54 / 54 test cases passed.
difficulty: medium
Runtime: 248 ms,beats 97%