BFS算法基本套路
本文默认读者是有一定算法基础的,对于基本的语法和bfs概念都了解,本文由浅入深(也不是很深咯),让你知道碰到bfs系列题目应该去怎么想,代码应该怎么去写,OK,直接进入正题。
基本bfs算法
这一部分是重中之重,因为在这里给出最基本bfs算法的写法,之后底下大部分的题,只是在这个基础上加一点东西罢了,所以这里的代码得牢记。
本文默认所有二叉树的定义如下:1
2
3
4
5# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
那么最基本的,用bfs算法去遍历一颗二叉树(bfs算法基本格式,很好记)1
2
3
4
5
6
7
8import collections
def bfs(root):
if not root: return
Q = collections.deque([root])
while Q:
node = Q.popleft()
if node.left: Q.append(node.left)
if node.right: Q.append(node.right)
以小见大,我们就从最基本的bfs算法中总结一下bfs算法的流程。
- 初始化队列,将起始点保存
- 节点依次出队列,并将出队列的节点的所有相邻节点加入队列
- 直至找到所求或队列遍历结束
bfs不仅用在树中,在二维数组(也可看成是一个图)中,也是经常使用的,正好利用上面总结的流程来看bfs算法在数组中怎么写
不妨设给定数组名为matrix,matrix[i][j]为起始点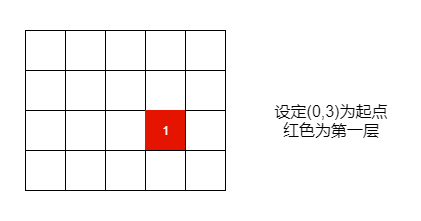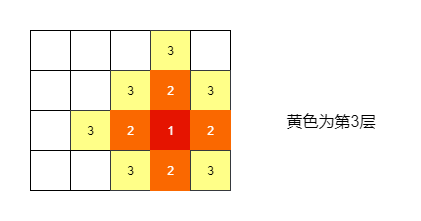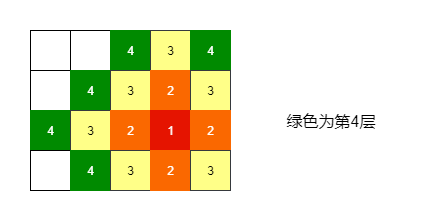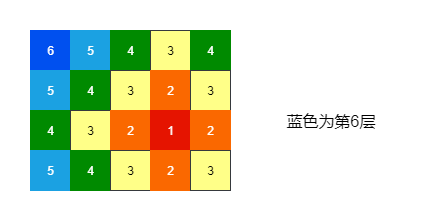
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15import collections
def bfs(i,j):
m,n = len(matrix), len(matrix[0])
visited = set((i,j))
# 初始化队列,保存起始点
Q = collections.deque([(i,j)])
while Q:
i,j = Q.popleft()
# visited.add((x,y))
# 所有相邻节点加入队列
for x,y in [(i+1,j),(i-1,j),(i,j+1),(i,j-1)]:
if 0<=x<m and 0<=y<n and (x,y) not in visited: # 未出界and不走回头路
Q.append((x,y))
# 注意visited一定要放在这里,不能是放在上面注释的地方,否则产生大量重复计算
visited.add((x,y))
OK,基本套路在心里有个印象,然后来看两个简单例子巩固一下
leetcode 107 Binary Tree Level Order Traversal
给定一棵树的根节点,按照自下而上的顺序依次输出每层节点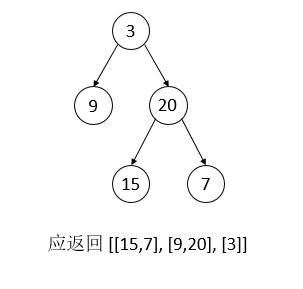
显然,这道题应用bfs进行遍历,但是需要一层一层的遍历,如何在遍历过程中知道现在这个节点是该层的最后一个节点呢?
这道题就体现了一个思路,每次记录一下当前队列的长度l,然后用一个长度为l的循环来pop node,循环结束时,刚好遍历完一层的节点1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16import collections
def bfs(root):
if not root: return []
Q = collections.deque([root])
res = []
while Q:
rec = [] # record all node in the same level
l = len(Q)
for i in range(l):
node = Q.popleft()
rec.append(node.val)
if node.left: Q.append(node.left)
if node.right: Q.append(node.right)
# 循环结束rec正好储存了该层的所有节点
res.append(rec)
return res[::-1]
leetcode 103 Binary Tree Zigzag Level Order Traversal
给定一棵树的根节点,按照zigzag顺序输出每层节点,即第一层节点从左至右,第二层节点从右至左,第三层节点从左至右,依次类推。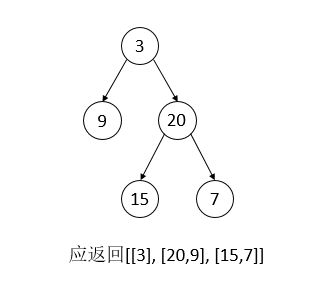
这道题和上道基本一样,无非是在处理某些层时,记录的节点顺序需要反转一下,引入一个level变量判定是否反转即可1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19import collections
def bfs(root):
if not root: return []
Q = collections.deque([root])
res = []
level = 1
while Q:
rec = [] # record all node in the same level
l = len(Q)
for i in range(l):
node = Q.popleft()
rec.append(node.val)
if node.left: Q.append(node.left)
if node.right: Q.append(node.right)
# 循环结束rec正好储存了该层的所有节点
if level % 2 != 0: res.append(rec)
else: res.append(rec[::-1])
level += 1
return res
上面两个跟树相关的bfs相对较为简单,因为对于总结的流程来说,二叉树通常有:
明确的起点,通常是根节点明确的相邻节点且不用考虑重复遍历的情况(因为单向)
但在更多的题目中却不是这样,不论是起始点还是相邻节点,都需要我们自己去分析判断才能得出。再来看下面两个例子,感受下这类题目如何去找流程中的两个关键点。
leetcode 542 01 Matrix
给定一个矩阵matrix(只包含0or1,保证至少有一个0),返回一个矩阵res,其中res[i][j]代表距离matrix[i][j]处最近的0的距离。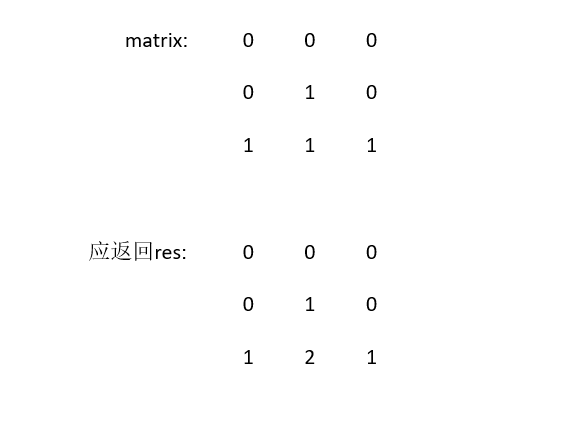
对于这道题,怎么找bfs的起始点呢,我们可能最初想到的是对每一个1都进行一次bfs遍历,去寻找与他最近的0的位置,但这样显然会超时,因为当1都聚集在一起的时候会有大量重复计算。
换个思路,既然1不行,那0行吗,以单个的0肯定不行,因为这个0找到的最近的1,并不一定是最短的,还得计算别的0然后来比较,所以还是得有大量重复计算和比较。
既然起始点找单个不行,我们可以找多个,我们将所有的0作为起始点,去找所有最后res[i][j]=1的点,然后将res=1的点作为起始点,去找所有最后res[i][j]=2的点,以此类推。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20def bfs(matrix):
m,n = len(matrix),len(matrix[0])
Q = collections.deque([])
visited = set()
# 初始化队列,将所有起始点加入
for i in range(m):
for j in range(n):
if matrix[i][j] == 0:
Q.append((i,j))
visited.add((i,j))
# 标准bfs写法,将相邻节点加入队列
while Q:
i,j = Q.popleft()
for x,y in [(i+1,j),(i-1,j),(i,j+1),(i,j-1)]:
if 0<=x<m and 0<=y<n and (x,y) not in visited:# 不出界 and 不走回头路
matrix[x][y] = matrix[i][j] + 1
# visited一定要在这里添加,否则产生大量重复计算
visited.add((x,y))
Q.append((x,y))
return matrix
leetcode 279 Perfect Squares
给定一个正整数n,找到m个平方数(1,4,9…)使得m个数的和为n,返回满足条件的最小的m
n = 12, return 3; because 12 = 4 + 4 + 4
n = 13, return 2; because 13 = 4 + 9
一般看到这道题大家第一反应可能是dp,记dp[i]表示组成和为i的平方数的最优个数,则dp[n]为所求。
递推式为:dp[n] = 1 + min(dp[n-1],dp[n-4],dp[n-9],...)
当然这是完全正确的,但是这里我们如果用bfs方法应该怎么做呢?
- 找起点,显然是n本身。
- 找相邻节点,显然为n-1,n-4,n-9,…,n-k^2,k满足(k+1)^2 > n。
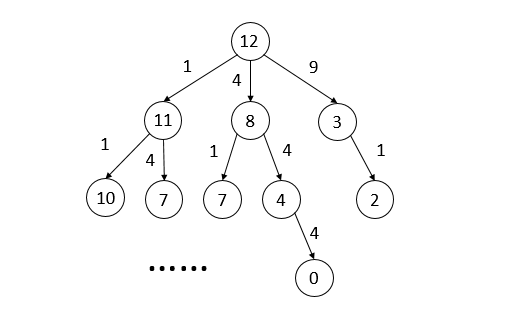
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16import collections
def bfs(n):
Q = collections.deque([n])
visited = set()
level = 0
while Q:
l = len(Q)# 按层处理
for i in range(l):
n = Q.popleft()
if n == 0: return level
for i in range(1,int(n**0.5)+1):# 遍历相邻节点 and 不重复计算
val = n - i**2
if val in visited: continue
Q.append(val)
visited.add(val)
level += 1
如果你看到这里觉得仿佛有点感觉了,那么建议你用这道题练一练
https://leetcode.com/problems/open-the-lock/description/
OK,截至到目前位置,我默认你应该对这种比较基础的bfs问题已经“一般”掌握了
所以我们稍微来看一点进阶的题目
leetcode 127 Word Ladder
给定一个word1和word2,和一个转换列表wlist,找出最短的变换路径使word1变成word2,其变换规则需满足:
- 一次只能改变word1中的一个字母
- 每次改变后的单词必须存在于wlist中
- 如果无法转换则返回0
word1 = “hit”,word2= “cog”
wlist = [“hot”,”dot”,”dog”,”lot”,”log”,”cog”]
return 5; because hit -> hot -> dot -> dog -> cog
相信你看了上面那么多题之后这道题应该不用我详细分析了吧,如图就完事了: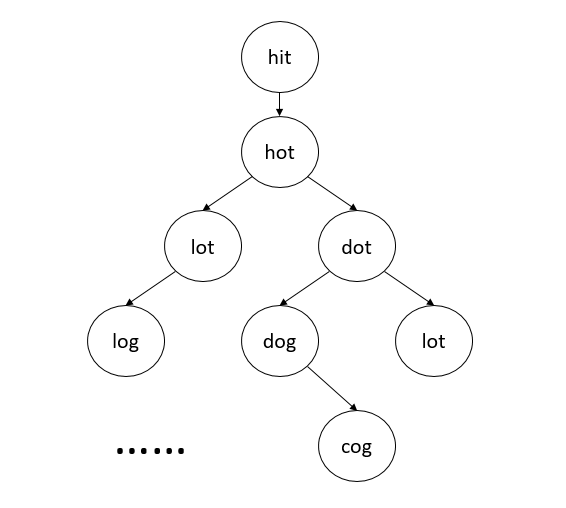
我们仍然根据之前说的bfs解题思路来分析:
- 找起始点,显然是word1
- 找相邻节点,显然是与当前单词只有一处地方不同的单词
那么我们得想办法保存一下每个单词的“相邻”单词。
例如对于’hot’,我们分别去找形如’_ot’,’h_t’,’ho_’ 的单词,又想到如果看到一个再去找一个复杂度也太高了,不如最初就把他们按照这种规则存在字典里面。
例如’hot’就分别存入d[‘_ot’],d[‘h_t’],d[‘ho_’]中,这样只花费了n*m个空间,其中n=len(wlist),m=len(wlist[0])1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26import collections
def bfs(word1,word2,wlist):
# 按照上述规则存储每个字符
d = collections.defaultdict(list)
visited = set()
for s in wlist:
for i in range(len(s)):
d[s[i:]+'_'+s[i+1:]].append(s)
# 初始化队列,将起点加入
Q = collections.deque([word1])
level = 1
while Q:
l = len(Q)
for i in range(l):
s = Q.popleft()
if s == word2: return level # 找到s
# visited.add(s)
# 添加相邻节点 and 不重复计算
for j in range(len(s)):
for s1 in d[s[:j]+'_'+s[j+1:]]:
if s1 not in visited:
Q.append(s1)
# visited一定要放在这,不能在上面注释的地方,否则产生大量重复计算
visited.add(s1)
level += 1
return 0
上面那道题关键就在如何保存相邻节点,而这其实是bfs问题中很关键的一环,我们再来看一道题,虽说被leetcode划分为hard,但我觉得应该只勉强够个medium,可以说还没有前面几道题难!
leetcode 815 Bus Routes
给定一系列的bus,其中bus[i]表示第i辆bus能经过的所有站,然后给定起始站和终点站,问从起始站出发需要换乘几辆车才能到达终点站。
bus = [[1,2,7], [3,6,7]]
start = 1,target = 6
return 2; because first take bus[0](1->7),then take bus[1](7->6)
Note:bus.length <= 500, bus[i].length <= 500, bus[i][j] < 10^6;
我们还是按照之前提到的bfs解题思路来分析:
- 找起始点,显然是start
- 找相邻节点,显然是当前站乘一次bus就可到的所有站,例如对于start,我们需要把bus里面所有含start的bus中的所有站设为start的相邻节点!
看到这里我们应该已经意识到问题所在了,如果我们把每个节点的相邻节点的保存下来的话,所需的空间实在太大了,从数据范围上可以看出,如果每个len(bus[i])=500,那么对于其中任意两个站a,b,都要有b in d[a] and a in d[b](也就是花费两个空间),那么总共就是Combs(500,2),再乘以500的话会超出空间限制!
那么这里应该怎么存呢?其实换个角度想,bus本身已经帮我们把每个节点的相邻节点存好了,只是没有放在一起而已,我们要做的应该是记录下对应的下标即可,例如对于测试样例中的站台7,我们应该保存(0,1),说明bus[0]和bus[1]中的所有节点都是站台7的相邻节点
1 | class Solution(object): |