Leetcode 891 Sum of Subsequence Widths

发表于 |

Given an array of integers A, consider all non-empty subsequences of A.
For any sequence S, let the width of S be the difference between the maximum and minimum element of S.
Return the sum of the widths of all subsequences of A.
As the answer may be very large, return the answer modulo 10^9 + 7.

Example 1:
Input: [2,1,3]
Output: 6
Explanation:
Subsequences are [1], [2], [3], [2,1], [2,3], [1,3], [2,1,3].
The corresponding widths are 0, 0, 0, 1, 1, 2, 2.
The sum of these widths is 6.
这道题还算有点意思

Note:

  1. 1 <= A.length <= 20000
  2. 1 <= A[i] <= 20000

分析：

  1. 首先我们需要明确，题目所求的widths和数组的本身的顺序没有关系，所以排序不会影响最后的结果，其次如果子串长度为1则widths为0，所以可以不用考虑
  2. OK，对于[1,2,3,4]这个数组，我们从第二个数开始分析：
    1. dp[1] = dp[0] + (2-1)*1 (对于nums[1] = 2)
    2. dp[2] = dp[1] + (3-1)*2 + (3-2)*1 (对于nums[2] = 3)
    3. dp[3] = dp[2] + (4-1)*4 + (4-2)*2 + (4-3)*1 (对于nums[3] = 4)
  3. 相信这么一写你肯定已经初步看出规律了，但是如果按照这个规律不做任何处理依次累加的话复杂度仍然是O(n^2)，肯定是不过关的，我们这里再写一下通用的式子吧:
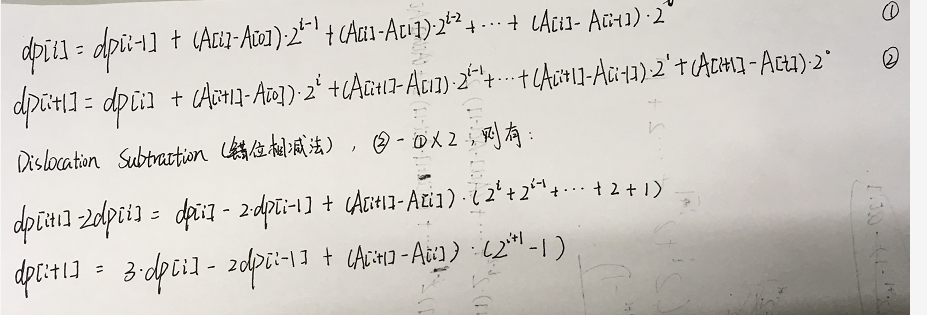
  4. 至此，递推式关系已出，显然dp[0] = 0, dp[1] = A[1]-A[0].

思路：

  1. 注意递推式中有一个2^(i+1)，因为这个i可以达到20000，所以我们必须先对所有2的次方进行预处理，也就是mod 1e9+7！(把这个作为全局变量，不要来一组数据又重新算一次)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
rec,mod,s = [],10**9+7,1
for i in range(20000):
    rec.append(s)
    s *= 2
    s %= mod

class Solution(object):
    def sumSubseqWidths(self, A):
        """
        :type A: List[int]
        :rtype: int
        """
        if len(A) < 2: return 0
        A.sort()
        dp = [0] * len(A)
        dp[0],dp[1] = 0,A[1]-A[0]
        for i in range(2,len(dp)):
            dp[i] = (3*dp[i-1] - 2*dp[i-2] + (A[i]-A[i-1]) * (rec[i]-1)) % mod
        return dp[-1]

64 / 64 test cases passed.
difficulty: hard
Runtime: 120 ms