Leetcode 918 Maximum Sum Circular Subarray

发表于 |

给定一个由整数数组 A 表示的环形数组 C，求 C 的非空子数组的最大可能和。
在此处，环形数组意味着数组的末端将会与开头相连呈环状。（形式上，当0 <= i < A.length 时 C[i] = A[i]，而当 i >= 0 时 C[i+A.length] = C[i]）
此外，子数组最多只能包含固定缓冲区 A 中的每个元素一次。（形式上，对于子数组 C[i], C[i+1], …, C[j]，不存在 i <= k1, k2 <= j 其中 k1 % A.length = k2 % A.length）

示例 1：
输入：[1,-2,3,-2]
输出：3
解释：从子数组 [3] 得到最大和 3

示例 2：
输入：[5,-3,5]
输出：10
解释：从子数组 [5,5] 得到最大和 5 + 5 = 10

示例 3：
输入：[3,-1,2,-1]
输出：4
解释：从子数组 [2,-1,3] 得到最大和 2 + (-1) + 3 = 4

示例 4：
输入：[3,-2,2,-3]
输出：3
解释：从子数组 [3] 和 [3,-2,2] 都可以得到最大和 3

示例 5：
输入：[-2,-3,-1]
输出：-1
解释：从子数组 [-1] 得到最大和 -1

提示：

  1. -30000 <= A[i] <= 30000
  2. 1 <= A.length <= 30000

题意分析：
这道题是要求数组连续和的最大值，但这里需要把数组看做是一个圆圈。是leetcode 53 Maximum Subarray的升级版！

思路分析：
我们可以直接将这个“圆圈”数组看做两个相同数组连接在一起

考虑到56题的情况，我们很容易想到将这道题分成两种情况来解决：
第一种情况即最大值就在第一部分中，第二种情况即最大值横跨两个部分但距离不得超过n，n为数组A的长度。分别如下图所示：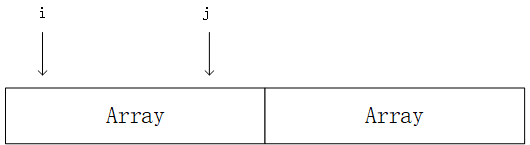

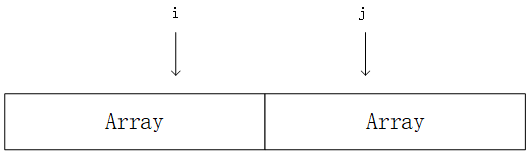
对于第一种情况，我们可以直接按53题的解法做

1
2
3
4
left = [A[0]] * len(A)
for i in range(1,len(A)):
    left[i] = max(A[i], left[i-1]+A[i])
res = max(left)

对于第二种情况，我们注意到数组一定经过A[-1]，对于某个左边界i，他能产生的最大和为
sum(A[i:]) + max(sum(A[n:j-n]) for every j < i+n)
显然每次都要找前缀和最大的值，我们使用一个数组将其保存以节省开销。
定义s[i] = sum(A[:i+1])
定义r_max[i] = max(s[:i+1])
则对于某个左边界i，他能产生的最大和为sum(A[i:]) + r_max(i)
完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution(object):
    def maxSubarraySumCircular(self, A):
        left = [A[0]] * len(A)
        s = [A[0]] * len(A)
        r_max = [s[0]] * len(A)
        for i in range(1,len(A)):
            left[i] = max(A[i], left[i-1]+A[i])
            s[i] = s[i-1] + A[i]
            r_max[i] = max(s[i], r_max[i-1])

        res = max(left)
        for i in range(len(A)):
            res = max(res, s[-1] - s[i] + r_max[i])
        return res