你的音乐播放器里有 N 首不同的歌,在旅途中,你的旅伴想要听 L 首歌(不一定不同,即允许歌曲重复)。请你为她按如下规则创建一个播放列表:
每首歌至少播放一次。
一首歌只有在其他 K 首歌播放完之后才能再次播放。
返回可以满足要求的播放列表的数量。由于答案可能非常大,请返回它模 10^9 + 7 的结果。
示例 1:
输入:N = 3, L = 3, K = 1
输出:6
解释:有 6 种可能的播放列表。[1, 2, 3],[1, 3, 2],[2, 1, 3],[2, 3, 1],[3, 1, 2],[3, 2, 1].
示例 2:
输入:N = 2, L = 3, K = 0
输出:6
解释:有 6 种可能的播放列表。[1, 1, 2],[1, 2, 1],[2, 1, 1],[2, 2, 1],[2, 1, 2],[1, 2, 2]
示例 3:
输入:N = 2, L = 3, K = 1
输出:2
解释:有 2 种可能的播放列表。[1, 2, 1],[2, 1, 2]
提示:
- 0 <= K < N <= L <= 100
题意分析:
总共有n首歌,要听l首歌,必须每首歌至少听一遍,若某一首歌需要听多遍的话,其中间的歌曲数量至少为k首。
思路分析:
在我的很多文中都提到过,看到mod 10^9+7,一定第一时间要想到dp。不说这种题目百分之百是dp,起码在leetcode上的题目基本全是。
那么怎么去分析呢?这道题一看像一个排列组合问题,熟悉排列组合的人对下面这个式子肯定不陌生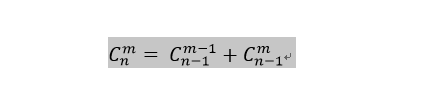
这个式子可以这样描述,在n个人里面挑选m个人,我们从挑不挑得到某个特定人X来考虑。
若挑得到,那么我们从剩下的n-1个人中再挑m-1个人。
若挑不到,那么我们从剩下的n-1个人中挑m个人。
这道题也是用类似的思路,我们定义f(n,l,k)为题目所求,则有:f(n,l,k) = f(n-1,l-1,k) \* n + f(n,l-1,k) \* (n-k)
其中f(n-1,l-1,k)代表某个特定的歌只最后出现一次,其余n-1首歌填充了前面l-1个位置,因为有n首不同的歌所以乘n。f(n,l-1,k)代表最后出现的某个特定的歌前面已经出现过了,这个最后出现的歌和当前最后k个位置的歌应当不相同,故乘(n-k)。
递推式已经找到,那么初始状态是什么呢?
显然当n==l时,则就是一个全排列,即为n!
当n > l or k > n时,都不存在解,故为0
注意到在递推式中k其实始终无变化,所以实际定义dp时k可以省去1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution(object):
def numMusicPlaylists(self, n, l, k):
mod = 10**9 + 7
# fib[n-1] = n!
fib = list(range(1,101))
for i in range(1, len(fib)):
fib[i] *= fib[i-1]
dp = [[0]*(l+1) for _ in range(n+1)]
for i in range(1,n+1):
for j in range(i,l+1):
if i == j: dp[i][j] = fib[i-1]
elif i < k: continue # 关键,否则(i-k) < 0
else:
dp[i][j] = dp[i-1][j-1] * i + dp[i][j-1] * (i-k)
return dp[-1][-1] % mod