2018.10.13 华为笔试

发表于 |

总结：共两道算法题，全部AC，两道题都是算法中的经典问题，一道标准dfs，一道约瑟夫环问题，还是比较有意思的。

1. 最大连通区域面积

在固定大小10x10的矩阵中，分布着若干个连通区域：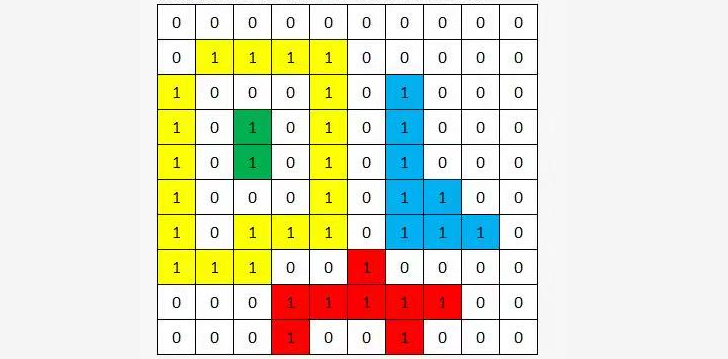

连通区域是由若干个相互连接的1方格组成，每个方格面积是1，求最大连通区域面积
如图所示，有4个连通区域，黄色面积为19，绿色面积为2，蓝色面积为8，红色面积为8，则最大面积为19.

输入描述：
100个数排成一行，由空格分割，输入中只包含0和1, 100个数是由矩阵按行从上到下依次排开的顺序输入。
上图中的输入数据为：0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 0 0 1 0 0 0 1 0 1 1 0 0 1 0 1 1 1 0 1 1 1 0 1 1 1 0 0 1 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 0 0 1 0 0 0

输出描述：
一个数字，表示最大连通区域面积

题意分析：
标准的dfs题型，对于每一个1，都使用一个dfs去遍历所有与其连通的1，已经遍历过的1则不处理，记录下每次dfs的最大值即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
s = input().split()
# 读入数据
grid = [[0]*10 for _ in range(10)]
for i in range(10):
    for j in range(10):
        grid[i][j] = int(s[i*10+j])

# dfs遍历面积
def dfs(i,j):
    ans = 1
    for x,y in [(i+1,j), (i-1,j), (i,j+1), (i,j-1)]:
        if 0<=x<10 and 0<=y<10 and grid[x][y] == 1 and (x,y) not in visited:
            visited.add((x,y))
            ans += dfs(x,y)
    return ans

res = 0
visited = set()
for i in range(10):
    for j in range(10):
        if grid[i][j] == 1 and (i,j) not in visited:
            visited.add((i,j))
            res = max(res, dfs(i,j))
print(res)

2. 餐桌(AC)

一个圆形餐桌上有n个人，编号从1到n（顺时针方向），编号1与编号n相邻
现在从编号1开始顺时针从1开始报数，每相邻而坐的就加1，报数为m则立即出局离开餐桌，出局后不能参与后面的报数，然后其顺时针方向的下一位重新从1开始报数。
这样一直报数，当餐桌上只剩一人，则该人自动出局，请你打印出这n个人离开餐桌的顺序

输入描述：
第一行一个整数t，表示测试样例的数量
对于每组测试样例：
第一行一个整数n，表示总人数 （1 <= n <= 1000）
第二个一个整数m，表示报到m的人出局 (1 <= m <= 1000)

输出描述：
对于每组测试样例：
输出一行n个数，空格隔开，表示离开餐桌的顺序

输入样例：
3
2
3
4
2
4
5

输出样例：
1 2
2 4 3 1
1 3 4 2

题意分析：
这是经典的约瑟夫环问题，通常来说这种题只用求最后胜出的那个人的编号，是可以用数学解法来求解，复杂度O(n)，但是这道题需要我们模拟出游戏的整个过程，那复杂度为O(m*n)，这道题n,m取值都不超过1000，故复杂度完全ok！

我们可以用队列来模拟整个过程，队列首部报数的人如果不是报的m，则重新加入队列尾部；否则直接丢弃，不参与之后的报数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from collections import deque
t = int(input())
for i in range(t):
    n = int(input())
    m = int(input())
    Q = deque(list(range(1,n+1)))
    cnt = 0
    res = []
    while len(Q) >= 1:
        val = Q.popleft()
        cnt += 1
        if cnt % m == 0:
            res.append(val)
        else:
            Q.append(val)
    print(' '.join(map(str, res)))