Leetcode 924 Minimize Malware Spread

发表于 |

在节点网络中，只有当 graph[i][j] = 1 时，每个节点i能够直接连接到另一个节点 j。
一些节点 initial 最初被恶意软件感染。只要两个节点直接连接，且其中至少一个节点受到恶意软件的感染，那么两个节点都将被恶意软件感染。这种恶意软件的传播将继续，直到没有更多的节点可以被这种方式感染。
假设 M(initial) 是在恶意软件停止传播之后，整个网络中感染恶意软件的最终节点数。
我们可以从初始列表中删除一个节点。如果移除这一节点将最小化 M(initial)， 则返回该节点。如果有多个节点满足条件，就返回索引最小的节点。
请注意，如果某个节点已从受感染节点的列表 initial 中删除，它以后可能仍然因恶意软件传播而受到感染。

示例 1：
输入：graph = [[1,1,0],[1,1,0],[0,0,1]], initial = [0,1]
输出：0
示例 2：
输入：graph = [[1,0,0],[0,1,0],[0,0,1]], initial = [0,2]
输出：0
示例 3：
输入：graph = [[1,1,1],[1,1,1],[1,1,1]], initial = [1,2]
输出：1

提示：

  1. 1 < graph.length = graph[0].length <= 300
  2. 0 <= graph[i][j] == graph[j][i] <= 1
  3. graph[i][i] = 1
  4. 1 <= initial.length < graph.length
  5. 0 <= initial[i] < graph.length

题意分析：
在一个图中，有某些节点初始处于被感染状态，随着时间的流逝最终会将所有直接或间接与该节点相连的节点全部感染。
现在可以修复一个初始感染节点，我们想使最终的感染节点数量最小，问该修复哪一个初始感染节点。

思路分析：
假设图结构如下图所示，初始感染节点为[1,3,5]，由黄色节点表示: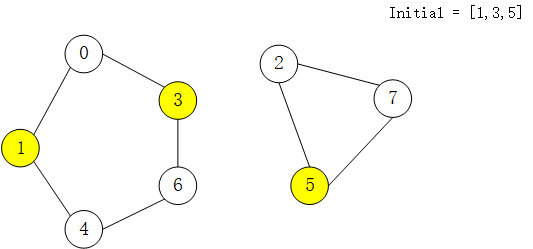

如果我们什么不操作，那么最终图上所有的节点都会被感染。
那我们现在想删一个初始感染节点，应该怎么去选呢？
假设删除1，最终左边这个连通子图还是会全部被感染，因为3是感染节点
删除3同删除1
假设删除5,可以使右边这个连通子图的所有节点不被感染，成功使感染节点少了3个

我们很容易发现，如果在一个连通子图里面，有两个或两个以上的节点初始被感染，那么无论我们删除哪个都对最后结果没有影响。我们唯一能使感染节点减少的操作就是删除那些只有一个感染节点的连通子图中的感染节点。

所以整个代码的逻辑应该如下：

  1. 找到一个连通子图
  2. 判断子图中感染节点的数量，若为1，执行第三步；反之执行第一步
  3. 计算该子图的长度，长度越长，就越可以最小化感染节点的数量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 188ms
class Solution(object):
    def minMalwareSpread(self, graph, initial):
        def dfs(node,vis):
            for v in  range(len(graph[node])):
                if graph[node][v] == 1 and v not in vis:
                    vis.add(v)
                    dfs(v,vis)

        s = set(initial)
        t_vis = set()
        del_node, subgraph_len = min(initial), 0
        for node in range(len(graph)):
            if node not in t_vis:
                vis = set([node])
                dfs(node,vis)
                # 计算子图中感染节点的数量
                infect = vis & s
                if len(infect) == 1:
                    # 长度更长 或者 长度相同但index更小
                    if len(vis) > subgraph_len or (len(vis) == subgraph_len and list(infect)[0] < del_node):
                        del_node,subgraph_len = list(infect)[0],len(vis)
                t_vis |= vis
        return del_node