在给定的二维二进制数组 A 中,存在两座岛。(岛是由四面相连的 1 形成的一个最大组。)
现在,我们可以将 0 变为 1,以使两座岛连接起来,变成一座岛。
返回必须翻转的 0 的最小数目。(可以保证答案至少是 1。)
示例 1:
输入:[[0,1],[1,0]]
输出:1
示例 2:
输入:[[0,1,0],[0,0,0],[0,0,1]]
输出:2
示例 3:
输入:[[1,1,1,1,1],[1,0,0,0,1],[1,0,1,0,1],[1,0,0,0,1],[1,1,1,1,1]]
输出:1
提示:
- 1 <= A.length = A[0].length <= 100
- A[i][j] == 0 或 A[i][j] == 1
题意分析:
在一个矩阵中,有两个岛(相连的1组成),找着两座岛的最短距离。
tips:看到找最短的xx问题,就一定要想到bfs。
思路分析:
我们从一个岛屿出发,用bfs遍历出所有相邻的矩形,直至和另一个岛屿有重叠的部分。如图: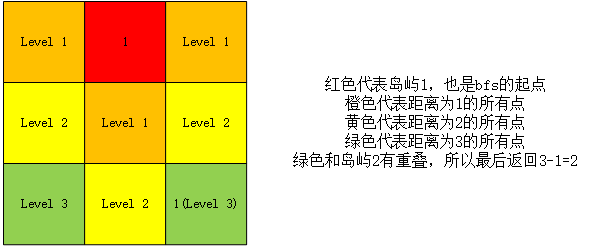

用dfs找出两个岛屿的所在地,用bfs获得最短距离1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36# 328 ms
class Solution(object):
def shortestBridge(self, A):
n = len(A)
def dfs(i, j, land):
for x,y in [(i+1,j), (i-1,j), (i,j+1), (i,j-1)]:
if 0<=x<n and 0<=y<n and A[x][y] == 1 and (x,y) not in land:
land.add((x,y))
dfs(x, y, land)
# dfs get two island
land1 = set()
land2 = set()
flag = 0
for i in range(n):
for j in range(n):
if A[i][j] == 1:
if (i,j) not in land1:
if not flag:
land1.add((i,j))
dfs(i, j, land1)
flag = 1
else:
land2.add((i,j))
dfs(i, j, land2)
# bfs get the shortest distance
Q = collections.deque(list(land1))
level = 0
while Q:
for _ in range(len(Q)):
i,j = Q.popleft()
if (i,j) in land2: return level - 1
for x,y in [(i+1,j), (i-1,j), (i,j+1), (i,j-1)]:
if 0 <= x < n and 0 <= y < n and (x,y) not in land1:
land1.add((x,y))
Q.append((x,y))
level += 1