leetcode 935 Knight Dialer

发表于 |

国际象棋中的骑士可以按下图所示进行移动：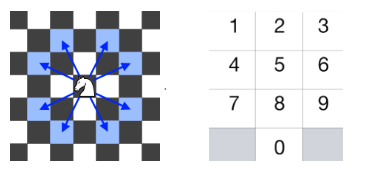

这一次，我们将 “骑士” 放在电话拨号盘的任意数字键（如上图所示）上，接下来，骑士将会跳 N-1 步。每一步必须是从一个数字键跳到另一个数字键。
每当它落在一个键上（包括骑士的初始位置），都会拨出键所对应的数字，总共按下 N 位数字。

你能用这种方式拨出多少个不同的号码？
因为答案可能很大，所以输出答案模 10^9 + 7。

题意分析：
一个骑士在电话拨号盘上连续行走N次，求总共可能走出多少种不同的电话。

tips：看到mod 1e9+7，就要想到dp

思路分析：
我认为这道题当你往dp方面去想的时候，就变得很简单，因为dp定义和递推式都显而易见。
定义dp[i][j]表示现在处于i位置，继续走j步所能走出的不同电话数量。
那么有dp[i][j] = sum(dp[nex][j-1] for nex in (i能走到的位置) )

使用一个字典d来保存每个位置所能到达的下一个位置。
初始化所有的dp[i][0] = 1，因为不能继续走，所以只有1种可能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 996ms
class Solution(object):
    def knightDialer(self, N):
        d = {0:[4,6],1:[6,8],2:[7,9],3:[4,8],4:[0,3,9],5:[],6:[0,1,7],7:[2,6],8:[1,3],9:[2,4]}
        dp = [[0]*10 for _ in range(N)]
        mod = 10**9 + 7
        for i in range(10): dp[0][i] = 1
        
        for i in range(1, N):
            for j in range(10):
                for nex in d[j]:
                    dp[i][j] += dp[i-1][nex]
                dp[i][j] %= mod
        
        return sum(dp[N-1]) % mod