Leetcode 943 Find the Shortest Superstring

发表于 |

给定一个字符串数组A，找出一个字符串S使得A中的每个字符串都是S的一个子串，并且使S的长度最短。

默认A中不存在某一个字符串是另一个字符串的子串。

Example 1:
Input: [“alex”,”loves”,”leetcode”]
Output: “alexlovesleetcode”
Explanation: All permutations of “alex”,”loves”,”leetcode” would also be accepted.

Example 2:
Input: [“catg”,”ctaagt”,”gcta”,”ttca”,”atgcatc”]
Output: “gctaagttcatgcatc”

Note:

  1. 1 <= A.length <= 12
  2. 1 <= A[i].length <= 20

思路分析：
这道题实际上是一个图的问题。
对于A = ["catg","ctaagt","gcta","ttca","atgcatc"]
不妨认为每一个字符串对应一个结点。边的权值则对应着两个结点之间重复部分的长度。
（0对应’catg’, 1对应’ctaagt,以此类推）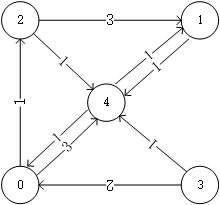

其中，G[2][1] = 3表示1结点若放在2结点后面可以省下3个字符长度。
最终，省得越多，最后的字符串长度就越短。

那么这道题就转换成了，在一个图中，从某个点出发将所有点恰好遍历一遍，使得最后路过的路径长度最长。（注意，虽然1,3之间没有连线但仍然可以从结点1走到结点3。）

首先我们将图构造出来

1
2
3
4
5
6
7
8
9
10
11
12
def getDistance(s1, s2):
        for i in range(1, len(s1)):
            if s2.startswith(s1[i:]):
                return len(s1) - i
        return 0

n = len(A)
G = [[0]*n for _ in xrange(n)]
for i in range(n):
    for j in range(i+1, n):
        G[i][j] = getDistance(A[i], A[j])
        G[j][i] = getDistance(A[j], A[i])

我们这里采用bfs的方法去遍历整个图，但如果不做任何处理，将所有情况全部考虑的话，共有12x11x10x...x1 = 12!种情况，时间复杂度过大。
稍微想一想，这其中有很多重复计算，例如对于这两个状态：

  1. 2->1->3->…
  2. 1->2->3->…
    同样是遍历了1,2,3这三个结点，并且当前都处在3结点上，我们是并不用将这两种情况都计算的。
    假设对于1->2->3我们计算出来已经走过的长度为L1，对于2->1->3我们计算出来已经走过的长度为L2，如果有L2 < L1，那么无论后面怎么走，第二种情况都不可能比第一种情况更优。所以我们可以舍弃掉第二种情况。

基于这个思想，我们使用一个空间d[mask][node]来记录当前状态下已经走的路程。其中：
mask表示当前已经遍历过的结点，10011表示已经遍历了0,1,4三个结点。（1 << i）
node表示当前所处结点。

在bfs中，这里采用了这样的结构(node, mask, path, repeat_len)。其中：
node表示当前结点
mask表示当前遍历过的结点
path表示遍历结点的顺序(长度不超过12，所以不用担心空间过大)
repeat_len表示目前重复部分的长度。

当mask == 11111时，表示已经遍历过所有结点，我们取此时repeat_len最大的path，然后通过path构造最后的字符串

例如path = [2,1,3,0,4]，那么构造函数如下：

1
2
3
4
5
6
def pathtoStr(A, G, path):
    res = A[path[0]]
    for i in range(1, len(path)):
        indice = G[path[i-1]][path[i]]
        res += A[path[i]][indice:]
    return res

全部代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution(object):
    def shortestSuperstring(self, A):
        def getDistance(s1, s2):
            for i in range(1, len(s1)):
                if s2.startswith(s1[i:]):
                    return len(s1) - i
            return 0

        def pathtoStr(A, G, path):
            res = A[path[0]]
            for i in range(1, len(path)):
                res += A[path[i]][G[path[i-1]][path[i]]:]
            return res

        n = len(A)
        G = [[0]*n for _ in xrange(n)]
        for i in range(n):
            for j in range(i+1, n):
                G[i][j] = getDistance(A[i], A[j])
                G[j][i] = getDistance(A[j], A[i])

        d = [[0]*n for _ in xrange(1<<n)]
        Q = collections.deque([(i, 1<<i, [i], 0) for i in xrange(n)])
        l = -1 # 记录最大的repeat_len
        P = [] # 记录对应的path
        while Q:
            node, mask, path, dis = Q.popleft()
            if dis < d[mask][node]: continue
            if mask == (1<<n) - 1 and dis > l:
                P,l = path,dis
                continue
            for i in xrange(n):
                nex_mask = mask | (1<<i)
                # case1: 不能走回头路，因为每个结点只能遍历一次
                # case2: 如果走当前这条路能够获得更大的重复长度，才继续考虑
                if nex_mask != mask and d[mask][node] + G[node][i] >= d[nex_mask][i]:
                    d[nex_mask][i] = d[mask][node] + G[node][i]
                    Q.append((i, nex_mask, path+[i], d[nex_mask][i]))

        return pathtoStr(A,G,P)