二分法基本套路
几个月没更新了,有点对不住,正好今天想没事找事,就来总结一下我写二分的一些经验吧。
本文主要会从这两个方面来介绍二分:
- 怎么看一道题是二分?
- 二分的代码怎么写(重点)
二分的基本使用
我们用一个复古的小游戏来解释一下
我从0到100随便想一个数X让你来猜,每次你猜一个数x我会告诉你X与x的大小关系,请问你会怎么猜。
当然这有点太简单了,我们都知道先猜50,然后根据结果每次对半猜。
为什么我们要猜50而不是60呢,有人一直会有这种想法,那就是假设猜60,万一我选的数是在60-100中岂不是加快了猜中的进程。
这其实就犯了一个哲学上的我也不知道叫什么的错误,那就是用一次或几次的结果(可能连续很多次我想的数确实在60-100当中)去推导普适性的结果。我们是在写一个算法,肯定是要应对各种情况嘛,并且你说每次不选mid而选一个奇怪的数,代码怎么写嘛。
有一点要记住,二分法关键在于舍去,每次舍去一半的答案,舍着舍着剩下的自然就是正确答案。
什么情况下用二分
对于我们做题来说,就是怎么看一道题是二分。
先给出结论,如果满足下面任意一个条件,则很有可能是二分:
- 从题意来看:题目给出一大堆限制条件,然后让你找一个数,这个数要满足那个条件
- 从数据范围来看:限制是O(nlogn)的解法
鉴于有很多没看过我以前题解的人,在这里再写一下数据范围相关的结论
n 达到 10^4,不能用O(n^2)
n 达到 5*10^6, 不能用O(nlogn)
也就是说,假设题目给一个 n < 10^6,那么很有可能是O(nlogn)的解法。
有人可能很好奇为什么数据范围能够作为判断复杂度的根据呢?像在topcoder和codeforces里面,很多题就是在卡数据范围,比如一道题有O(n)的解法,那么数据一定会卡到你必须用O(n)才能过的地步,很少会让你O(nlogn)偷掉。
当然这个卡数据是非常难的,因为logn是一个很小的数据,即使n达到了10^9,logn也才30,你要算也才O(30n)而已。在leetcode上没有严格的这种数据限制,第二点更多的当成一个trick吧。
等下我们一边看例题,一边体会刚才说的这两点,不过在此之前,我们先来记一下二分的基本写法
二分的基本写法(超级重要)
简单例题1
给定一个有序数组nums,给定一个整数A,找出A在nums数组中的下标。数组中每个元素只出现一次,保证A在数组中。
这个应该是非常简单了,我直接给出代码,这份代码你可以看成是二分法的写法模板,一定要理解之后再往下看。1
2
3
4
5
6
7
8
9
10
11
12
13
14def binarySearch(nums, A):
n = len(nums)
lo, hi = 0, n-1
def check(mid):
return nums[mid] < A
while lo < hi:
mid = lo + (hi - lo) // 2
if check(mid):
lo = mid + 1
else:
hi = mid
return lo
看完这个代码你可能会有很多问题
q1:为什么求mid要写成
lo + (hi - lo) // 2而不是(lo + hi) // 2呢
a1:防止lo+hi过大导致的溢出,当然在python里面是不会溢出的,主要针对c++,java,go这种需要声明类型的语言
q2:就判断一下nums[mid]和A的大小关系,为什么要写成check函数
a2:这其实是为了主体部分(while lo < hi)中代码的整洁性,抽象成统一模板,以后每次变动只要变check函数就行了
q3:在循环过程中,如果
nums[mid]==A就没必要再循环了啊,可以直接return,你这个代码里面相当于多循环了很多次啊,我觉得应该写成这样
2
3
4
5
6
7
8
mid = lo + (hi - lo) // 2
if nums[mid] == A:
return mid
elif nums[mid] < A:
lo = mid + 1
else:
hi = mid
a3:从逻辑正确性上来说这样写当然没有问题,但是
在循环内返回结果是一个非常不好的习惯,很容易踩坑,等下用例题解释一下。至于多循环了很多次,这个不至于,因为说过logn很小,总共循环不到30次,你提前或者晚一点结束影响真不大。
q4:最后为什么返回lo,不返回hi啊?
a4:最后lo必等于hi,返回谁都一样
好起来了,通过这个例子来以小见大,我们就来总结一下二分法的步骤
定二分范围的上下界确定check()函数,以此调整lo,hi的变化模式循环外返回结果
以上面的例题来解释:
先定上下界。因为我们要求的是下标,所以范围自然是[0, n-1],n为数组长度。
确定check()函数。我们找到一个数,依靠什么来判断来舍去一部分的答案呢,题目中提到是有序数组,所以可以按照大小来区分。
循环外返回结果。这里求下标,我们直接返回即可,但在大部分情况下却不仅仅是这样。
简单例题2
给定一个有序数组nums,给定一个整数A,找出A在nums数组中的下标,若存在相同元素则返回最大的下标值。数组中每个元素可以出现多次,保证A在数组中。
example:
nums = [1, 2, 3, 3, 3, 5], A = 3
return 4; because nums[4] = 3
思路分析:
显然仍然是二分,不妨设最终答案所在位置为Index,我们每次使用二分找到的位置为index。那么若nums[index] <= nums[Index],则说明index <= Index,通过这一点确定lo,hi的变换情况
1 | def binarySearch(nums, A): |
嚯嚯,这段代码有东西了,细心一点的话应该注意到了和上一段代码的不同吧
不同点1: 上一个是 lo=mid+1, hi=mid,而这个是lo=mid, hi=mid-1
不同点2: 上一个是mid=lo+(hi-lo)//2,而这个是mid=lo+(hi-lo+1)//2
为什么会有这两个不同呢?
- 对于第一个不同,那是因为题意的原因,我们发现
nums[mid]<=A时说明此时的mid应当在正确答案的左边,所以我们要在右边(也就是[mid,hi]中)搜,并且由于此时mid可能就是正确答案,所以mid本身不能跳过 - 对于第二个不同,是由第一个不同导致的,来看例子奥
假设lo = 3, hi = 4。 代码中lo,hi变换情况为check为true -> lo=mid, 为false -> hi=mid-1
若mid=lo+(hi-lo)//2, mid = 3,check(3)一旦为true,则lo = 3, hi = 4此时陷入死循环!!!
若mid=lo+(hi-lo+1)//2, mid = 4,此时check(4)为true or false都能成功结束。
不信的兄弟萌用这个例子去检验一下nums = [1, 2, 3, 3, 3, 5], A = 3
额外思考一下:如果在循环内返回答案,想想这个代码有多难写!
来做题咯!
leetcode 34 Find First and Last Position of Element in Sorted Array
给一个有序整数数组nums,给定一个target,找出target出现的第一个以及最后一个的位置
如果找不到返回[-1, -1]
example 1
input: nums = [5,7,7,8,8,10], target = 8
output: [3, 4]
example 2
input: nums = [5,7,7,8,8,10], target = 6
output: [-1, -1]
思路分析:
其实就是上面的讲的例题,无非是多了个求左边,并且多判断一下找的数是不是存在数组中
直接上代码1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution(object):
def searchRange(self, nums, target):
if not nums: return [-1 ,-1]
# 定上下界
lo, hi = 0, len(nums)-1
# 先找最左边的位置,根据check函数定lo,hi变化,从而确定mid求法
def check1(mid):
return nums[mid] < target
while lo < hi:
mid = lo + (hi-lo) // 2
if check1(mid): lo = mid + 1
else: hi = mid
# 若不存在返回
if nums[lo] != target: return [-1, -1]
l = lo
# 定上下界
lo, hi = 0, len(nums)-1
# 再找最右边的位置,根据check函数定lo,hi变化,从而确定mid求法
def check2(mid):
return nums[mid] <= target
while lo < hi:
mid = lo + (hi-lo+1) // 2
if check2(mid): lo = mid
else: hi = mid - 1
r = lo
return [l, r]
可以看到其实我们是用了两次二分去找两个边界,这个思路是没有问题的,但python代码肯定不能写得这么又臭又长,我们可以直接用标准库(bisect)来解决奥1
2
3
4
5
6
7
8
9
10
11
12# O(logn) time, O(1) space, 14, 9
class Solution(object):
def searchRange(self, nums, target):
if not nums: return [-1 ,-1]
# bisect_left可以获得target插入nums中的位置,若有相同元素则返回最左边的位置
# bisect_right则是返回最右边的位置
# 例 nums = [1,2,2,3], target = 2
# 则bisect_left(nums, target) = 1; bisect_right(nums, target) = 3
l = bisect.bisect_left(nums, target)
if l >= len(nums) or nums[l] != target: return [-1, -1]
r = bisect.bisect_right(nums, target)
return [l, r-1]
来看一道不是下标的
leetcode 875 Koko Eating Bananas
给定n盘香蕉,第i盘里有piles[i]根香蕉,现在有H个小时让koko来吃这些香蕉。
koko每小时能吃K根香蕉,但koko每小时只能选择一盘香蕉吃,这代表即使那盘香蕉不足K个,koko在这个小时内也不能去吃其他盘里的香蕉了。
koko想把所有的香蕉全部吃完,求K的最小取值。
数据满足n <= H, n <= 10^4, piles[i] <= 10^9
example 1:
input: piles=[3,6,7,11], H=8
output: 4
思路分析:
求什么?求一个数。
什么数?能让koko在规定时间内吃完香蕉的数,越小越好
数据范围n达到10^4,不能使用O(n^2)的解法。
有二分内味儿了!那我们就按照二分的基本步骤来解这道题
- 定上下界。我们要明确我们找的是吃的速度,那么最低,起码得在吃吧,所以起码
lo = 1,那hi呢?我们注意到n <= H,因为我们吃的速度就算再快,一次也只能吃一盘而已,所以无论怎样最少都得n个小时才能吃完,所以hi = max(piles) - 定check()。对于我们找的一个速度mid,我们可以算出按照这个速度吃,要吃完全部香蕉需要多少时间。若所需时间大于H小时,说明吃得慢了,应该更快一点,接下来从[mid,hi]中找。反之,则说明吃完时间还绰绰有余,还可以吃慢一点,从[lo, mid]中继续找
- 循环外返回结果,由于所求即为速度,直接返回lo即可
1 | # O(nlogm) time, m = max(piles), O(1) space, 13, 5, 14 |
继续来看
2019.03.16头条笔试第四题
有N根绳子,第i根长度为L[i],现在需要M根登场的绳子。
你可以对这N根绳子进行任意裁剪(不能拼接),请你计算出这M根绳子最长的长度(结果保留两位小数)
数据范围 1 <= N,M <= 10^5, 0 < L[i] < 10^9
example 1:
input: L = [3, 5, 4], M = 4
ouput: 2.50;第一根和第三根绳子分别裁剪出一根2.50长度的绳子,第二根绳子刚好可以裁剪出两根2.50的长度绳子,刚好4根。
思路分析:
求什么?求一个数
什么数?按这个数裁剪能得到M根绳子,这个数越大越好
数据范围N达到10^5,不能使用O(n^2)的解法。
又有二分内味儿了,按基本步骤来一步一步分析
- 定上下界。裁剪后的最大的长度不可能超过最长的绳子的长度吧,hi = max(L)。最小呢,或许可以很小很小,无限接近于0,因为可以取小数,不妨就定为0。
- 定check()。对于我们找的一个长度mid,我们可以算出按照这个长度去裁剪,最多能裁出多少根绳子。若裁出的总数大于M,说明现在选择的长度或许还可以更长,接下来在[mid,hi]中找,反之在[lo,mid]中找。
- 循环外返回结果,由于所求即为长度,直接返回即可。
1 | # O(mlogn) time, m = max(L), O(1) space, 19, 8, 9 |
如果你看到这里已经觉得有点感觉了,可以拿这道题练练手
https://leetcode.com/problems/heaters/
go on,这次看一道稍微难一点点的题目
leetcode 878 Nth Magic Number
给定两个数A,B,如果一个数能整除A或整除B,我们将这个数称为”magical number”
找出第N个’magical number’,答案可能非常大,需要mod 10^9+7
Example 1:
Input: N = 1, A = 2, B = 3
Output: 2; magical number is 2, 3, 4, 6, …
Example 2:
Input: N = 4, A = 2, B = 3
Output: 6; magical number is 2, 3, 4, 6, …
Example 3:
Input: N = 5, A = 2, B = 4
Output: 10; magical number is 2, 4, 6, 8, 10, …
Example 4:
Input: N = 3, A = 6, B = 4
Output: 8; magical number is 4, 6, 8, 12, 16, 18, …
数据范围: 1 <= N <= 10^9, 2 <= A,B <= 40000
思路分析:
嘻嘻,我的老观众都知道,当题目中出现mod 10^9+7的时候,这道题八成是dp,但是这道题并不是,相信你们也可以从数据范围看出来
那这道题怎么就是二分呢?这是怎么看出来的
求什么?求一个数
什么数?这个数必须要能整除A or B,并且还必须是第N个满足这个条件的数
那问题来了,对于一个数,你怎么知道他是第几个magical number?
其实这个问题可以转换成,是不是恰好有n-1个magical number比当前数小!
我们先只看一个数,假设A=2,我找的数是8,问8是第几个magical number,显然2,4,6,8,…,应该是第4个。 4是通过8//2得出来的对吧。
那再来看两个数,假设A=2,B=3,我找的数是8,问8是第几个magical number。
首先8//2 + 8//3 = 6,那8是第6个吗? 2,3,4,6,8,…,显然不是,算成第6个是因为我们把6这个数字算了两遍,我们应该要减去这些重复的数,也就是A,B的公倍数。具体有多少个公倍数可以通过8//最小公倍数来计算。(不会有憨猪不知道最小公倍数怎么算吧。)
有一个要注意的地方, look this picture
对于mid落在1位置的情况,只有n-1个magical number小于等于mid,此时应该lo = mid+1
对于mid落在2位置的情况,有n个magical number小于等于mid,此时应该hi = mid
1 | # O(log10**14) time, O(1) space, 8, 1, 14 |
leetcode 778 Swim in Rising Water
给定一个NxN的网格grid,请你找到一条道路,从(0,0)出发一直走到(n-1,n-1),使得这条路上的最大值最小。
网格中的数从0,n^2-1各一个。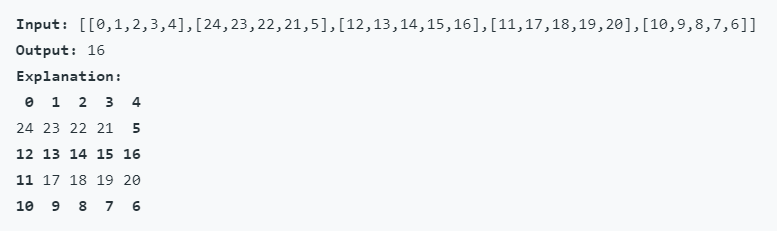
思路分析:
是在找数吧,这个数要满足一定条件吧,二分走起
1.定上下界。下界起码是起点的大小,grid[0][0],因为起点是必走的,上界应该是网格中的最大值。
- 定check()。check(mid)定义为路径上最大值不超过mid的情况下能否从(0,0)走到(n-1,n-1)。若为true,代表或许现在能走到,可能还能更小,应该hi = mid,反之lo = mid
- 循环外返回结果,直接返回即可。
当然check(mid)涉及到dfs的解法了,这里的dfs不难奥,就是单纯的带限制条件的在grid里面走而已。
实在不懂也没关系,因为我马上要出dfs详解了,到时候回来看一下就好了。
1 | # O(n^2logn^2) time, O(n^2) space, 26, 8, 21 |
本文顺手隐藏了个彩蛋,有兴趣的兄弟萌可以找一找。