Recursion套路

兄弟萌，这个真的特别重要，这个要是会了，dfs, backtracking就都会了。

什么是递归？

explanation from baike:
递归,就是在运行的过程中调用自己。构成递归需具备的条件:

子问题须与原始问题为同样的事,且更为简单;
不能无限制地调用本身,须有个出口,化简为非递归状况处理。

talk is cheap, show me the code.
斐波那契数列大家都知道，就是下一项等于前两项的和，形如
1, 1, 2, 3, 5, ...
请问，这个数列的第30项是多少呢？当然我们可以很轻松的写出这样的代码：

def getNthFib(n):
    if n == 1 or n == 2: return 1
    return getNthFib(n-1) + getNthFib(n-2)

print(getNthFib(30))

当然，实际有更好的写法，这里我们先不考虑，就看这段代码。对于斐波那契数列来说，这样的求解方式完美契合了上面说的递归条件吧，每个子问题都比原问题更为简单（n越来越小），不能无限制地调用自身（n=1 or n=2停止递归），那么这就是一个最简单的递归示例。

我们直接来以小见大，写递归需要：

找到问题与子问题的关系，且子问题通常更简单
需存在终止条件，且子问题最后能够走到终止条件

那有人就会问了，我怎么去找一个问题的子问题呢？确实，这是一个不算简单的事，但也没那么难，先看下面这段话。

在我给很多人讲递归问题的过程中，我发现大家都有一个通病，就是对递归过程总是很迷糊，总觉得想不清楚，非要用一组数据对着代码一句一句去检验。（别以为你看懂了上面的那个例子就觉得你没有这个毛病）

我自己最初也是这样，所以我特意针对这个问题分析了一下，关键点就在于函数定义，这就仿佛高中数学里面的通项公式，我们是根据定义来写代码的，这样空说或许很难懂，我们就以上面这段代码来解释说明。

我们要求什么？斐波那契数列里面的第30个数，那我们定义getNthFib(n)代表斐波那契数列里面的第n个数，这样最后返回getNthFib(30)即可。

根据斐波那契定义，第n个数 = 第n-1个数 + 第n-2个数，转换成我们定义的函数getNthFib(n) = getNthFib(n-1) + getNthFib(n-2)，那么关系就找出来了，接下来看终止条件，我们发现n每次减少1or2，最后一定会减到1或者2，终止条件定n==1 or n==2即可

那现在回到刚才的问题，怎么去找一个问题的子问题？
其实就是去找定义，根据你的定义来get子问题，有时候我们定义的函数直接就是所求，而有时候又不是，需要我们自己去思考。

在看例题之前再重申一下：关键在定义！定义！根据定义写推导式和终止条件，写完就直接结束，千万别一个一个拿数据再去代。

leetcode 100 Same Tree

给定两棵树的根结点p,q，判断这两棵树是否相同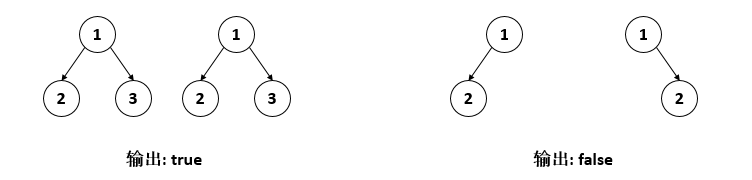

思路分析：
我们怎么去比较两棵树是不是相同，那肯定是每个结点都比一下嘛，那是不是先看下根结点是否相同，如果根结点不相同下面的节点也不用看了。那比完根结点，再看下左子树是不是相同，再看下右子树是不是相同。

定义：isSame(p, q)代表以p,q为根结点的两棵树是否相同，函数返回值类型为bool，根据定义则有（注意代码内的序号，代码的实际书写顺序应按照序号书写）

def isSame(p, q): # return type = bool
    # 3 根据“函数”定义确定终止条件
    # 两棵树都为空，那肯定是相同的，一个空一个不空，肯定不同
    if not p and not q: return True
    if not p or not q: return False

    # 1. 根结点若不同直接返回false
    if p.val != q.val: return False
    # 2. 根结点相同的情况下，左子树必须相同且右子树也必须相同
    return isSame(p.left, q.left) and isSame(p.right, q.right)

在这里重复一遍，根据定义写推导式和终止条件，写完就直接结束，千万别一个一个拿数据再去代。

是不是没看懂？不急不急，多看两道，多看两道就有感觉了。

leetcode 112 Path Sum

给一颗二叉树和一个数target，问是否存在一条从根结点到叶子结点的路径，使得路径和等于target.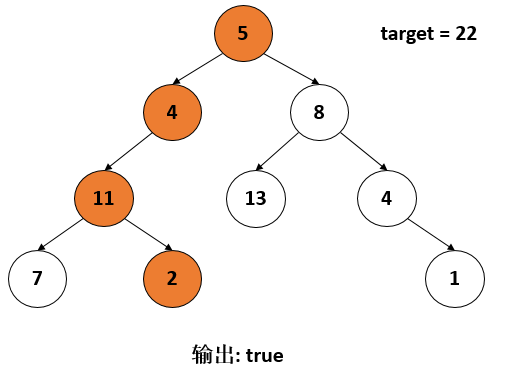

思路分析：
让我们找一条从根结点到叶子结点的路径，第一反应应该是dfs，也确实就是dfs，只是说我们从定义的角度去写。

那怎么定义呢，我们稍微分析一下题目，这条路径要从根结点出发，那么根结点的值一定在路径中吧，以示例来说，这道题是不是可以看成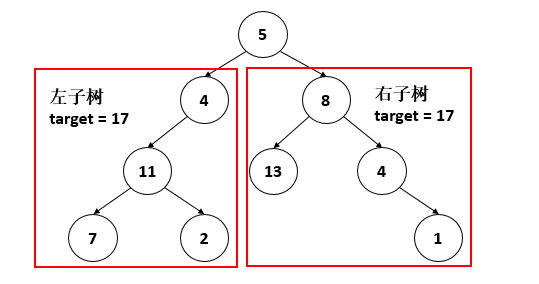

那么显然，定义：dfs(root, target)表示在以root为根结点的树中，能否找到一条从根结点到叶子结点的路径，使得路径和等于target，函数返回值类型为bool
则有 dfs(root, target) = dfs(root.left, target-root.val) or dfs(root.right, target-root.val)

代码如下，注意序号，代码的实际书写顺序应按照序号书写

def dfs(root, target): # return type = bool
    # 3. 根据函数定义确定终止条件
    # 要找路径，连路都没有的话，自然找不到
    if not root: return False

    # 1. 如果当前结点为叶子结点，判断结点值是否等于target
    if not root.left and not root.right and root.val == target:
        return True

    # 2. 当前结点不是叶子结点，则从左右子树中继续寻找答案
    l = dfs(root.left, target - root.val)
    r = dfs(root.right, target - root.val)
    return l or r

注意奥，终止条件可不是随便写的，要保证两点原则，那就是
条件：if not root是通过递推式确定的，要保证参数值能走到这个条件里
结果：return False是通过函数定义来确定的，在root为空的条件下，根据函数的定义，我们应该返回false
还不懂？别急别急，先继续看。

leetcode 113 Path Sum II

给定一颗二叉树和一个数target，请找出所有从根结点到叶子结点的路径，使得路径和等于target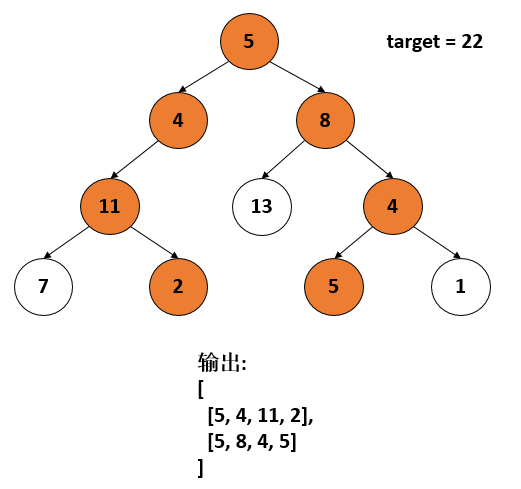

思路分析：
和上道题一样的吧，根结点是肯定要的，所以在左右子树中继续去寻找路径，不过之前定义的函数是返回bool，这次返回的应该是一个二维list

定义：dfs(root, target)表示在以root为根结点的树中，所有从根结点到叶子结点的路径，使得路径和等于target，函数返回值为二维List.

对于子树中找到的全部路径，我们可以在里面每个路径前都加上root.val来获得结果

以示例来说，就比如两个子树中找到了这样的路径构成17，
[
[4, 11, 2],
[8, 4, 5]
]
只要依次在前面加上5，即可得到最后的答案，看代码

def dfs(root, target): # return type = List[List[int]]
    # 3. 根据函数定义确定终止条件
    # 找所有路径，都没路的话，自然找不到，注意返回的是空的二维list
    if not root: return []

    # 1.当前为叶子结点且值为target，返回结果，注意是二维List
    if not root.left and not root.right and root.val == target:
        return [[target]]

    # 2.对子树中找到的路径，在每个路径前面加上当前的val值
    res = []
    for path in dfs(root.left, target-root.val) + dfs(root.right, target-root.val):
        res.append([root.val] + path)
    return res

还没感觉真说不过去了奥，起码对于树相关的题目应该明白了吧
为什么说对于树呢，因为树相关的题递推关系好找，通常就在结点与子结点之间找，而且函数定义也是求什么就定义什么，来检验一下自己吧

https://leetcode.com/problems/maximum-depth-of-binary-tree/

下面看个数组的

leetcode 78 Subsets

给一系列不同的整数，返回所有的子集。

example 1:
input: nums = [1, 2, 3]
output: [[], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3]]

思路分析：
问：已知[2, 3]的全部子集是 [[], [2], [3], [2, 3]]，怎么获得[1, 2, 3]的全部子集

答：[1, 2, 3]的子集可以拆分成包含1和不包含1的两部分，其中不包含1的部分就是[2, 3]的全部子集，包含1的部分就是在[2,3]的子集里全部加1。即
[[], [2], [3], [2, 3]] + [[1], [1, 2], [1, 3], [1, 2, 3]]

基于这个结果，我们定义dfs(nums)表示nums的全部子集，函数返回值为二维list

def dfs(nums): # return type = List[List[int]]
    # 2. 根据定义确定终止条件
    # 空集是任何集合的子集，注意要返回二维列表
    if not nums: return [[]]
    
    # 1. 对nums[1:]的每个子集subset，将其‘自身’和‘自身加上nums[0]’加入结果
    res = []
    for subset in dfs(nums[1:]):
        res.append(subset)
        res.append([nums[0]] + subset)
    return res

当然，实际每次对数组做切片操作消耗代价有点大，通常以下标来表示取的数组的哪个区间
定义dfs(index)表示nums[index:]数组的全部子集，那么dfs(0)即为所求

# nums = [1, 2, 3]
def dfs(index):
    if index == n: return [[]]

    res = []
    for subset in dfs(index+1):
        res.append(subset)
        res.append([nums[index]] + subset)
    return res

n = len(nums)
return dfs(0)

其实有没有发现，数组找关系也差不多，nums与nums[1:]之间找，或者nums[i:j]与nums[i+1:j]和nums[i:j-1]找

handrew ph, do you understand now?

未完待续~